刚开始做研究的学习笔记，仅供参考

基本知识

不经意传输(Oblivious Transfer 或 OT)

1-out-of-2

我们主要关注1-out-of-2 oblivious transfer，写作$OT_1^2$。发送方Alice有两条消息 $x_0, x_1 \in \{ 0,1 \}^l$，而接受方Bob想知道其中的一个$x_b, b \in \{0,1\}$。不经意传输的目的是使接受方得知$x_b$，却不知道另一个$x_{1-b}$，而发送方不能得知$b$。

我们可以借助离散对数问题来实现OT，原理类似Diffie–Hellman。双方已知大质数$p$（第三步需要 bitwise XOR）以及原根$g \in \Z_p$x_0,x_1 \in \Z_p$。

1. Alice 随机生成$s, r_0, r_1$，发送给Bob $g^s$

2. Bob 随机生成$k$，发送给 Alice $h = \begin{cases} g^k & b=0 \\ g^{s-k} & b = 1 \end{cases}$

3. Alice 计算 $y_0 = h^{r_0} \oplus x_0, y_1 = (g^s / h)^{r_1} \oplus x_1$，把$g^{r_0}, y_0, g^{r_1}, y_1$都发给Bob

4. Bob 根据 $b$ 解密

   • $b=0$:

     $$(g^{r_0})^k \oplus y_0 = g^{r_0 k} \oplus g^{k r_0} \oplus x_0 = x_0$$

   • $b=1$:

     $$(g^{r_1})^k \oplus y_1 = g^{r_1 k} \oplus (g^s / g^{s-k})^{r_1} \oplus x_1 = g^{r_1 k} \oplus g^{k r_1} \oplus x_1 = x_1$$

这里由于离散对数问题没有高效解法，中间发送的$g^s,h,g^{r_0},g^{r_1}$并不会泄露$s,k,r_0,r_1$。证明暂略。

还有很多其他实现，比如The Simplest Protocol for Oblivious Transfer，wiki上还有用RSA的实现。另外，我们也可以使用OT传输密钥，再用对称加密（如AES）加密消息，来实现跟搞效率传输长信息。

1-out-of-n

有了 1-out-of-2 我们就可以实现 1-out-of-n 的OT，这里我们介绍一种简单的需要$n$次$OT_1^2$实现。

1. Alice 对$j=1,...,n$随机生成$k_j \in \{0,1\}^l$，并令$k_0=0^l$。
2. Alice 向 Bob发送$n$次$OT_1^2$，第$j$次Alice提供$(\oplus_{i=0}^{j-1} k_i) \oplus x_j$和$k_j$，Bob只在第$b$次选择前者，其他情况下都选择后者。
3. Bob通过前$b-1$次OT获取$k_1,...,k_{b_1}$，结合第$b$次的$(\oplus_{i=0}^{b-1} k_i) \oplus x_b$得到$x_b$。

此外还有$\log n$的算法

OT-Extension

TODO

Corrlated OT

TODO

混淆电路(Yao's Garbled Circuits Protocol)

混淆电路可以让双方在不知晓对方输入的情况下，共同计算一个电路的输出。协议在semi-honest也就是honest-but-curious环境下是安全的，攻击者会在遵守协议的情况下尽可能的多获取信息。我们之后介绍到的应用场景下，协议双方很可能是在公司或政府机构，所以比较适合semi-honest环境。我们也可以通过加入零知识证明等工具改进协议，实现对恶意攻击的安全性。

同样我们需要一个发送方Alice和接受方Bob，各自拥有输入的一部分，而电路（也就是我们要计算的函数）对双方是公开的。

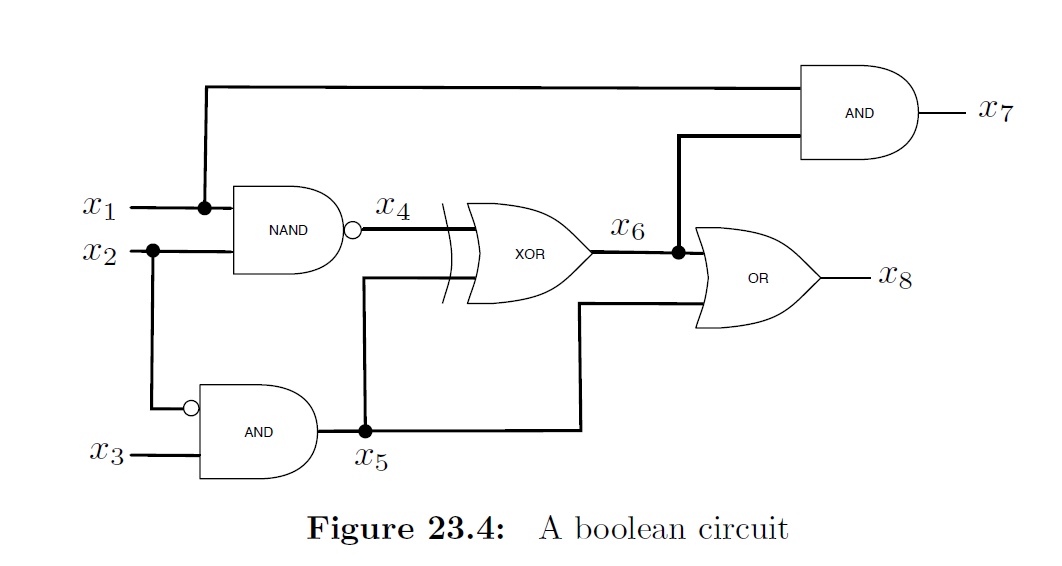
我们需要为电路中的所有“线”(wire)编号，比如图中$x_1, x_2, x_3$是输入，$x_7,x_8$是输出，而$x_4,x_5,x_6$是中间值。Alice可能持有$x_1,x_3$的值而Bob持有$x_2$的值，而我们的目的是在Alice不知道$x_2$，Bob不知道$x_1,x_3$的情况下，让双方合作算出$x_7,x_8$。

混淆电路的协议分为以下几步：

1. Alice生成混淆电路，并发送给Bob。

   Alice对于每个$x_i$生成随机密钥$X_i^0, X_i^1$，代表每条线可能的取值。对于电路中的每个门，把输入替换为对应随机密钥，把输出对应的随机密钥用输入加密。比如图中的OR，本来是

   $x_5$	$x_6$	$x_8$
   0	0	0
   0	1	1
   1	0	1
   1	1	1

   我们需要替换为

   $x_5$	$x_6$	$x_8$
   $X_5^0$	$X_6^0$	$E_{X_5^0, X_6^0}(X_8^0)$
   $X_5^0$	$X_6^1$	$E_{X_5^0, X_6^1}(X_8^1)$
   $X_5^1$	$X_6^0$	$E_{X_5^1, X_6^0}(X_8^1)$
   $X_5^1$	$X_6^1$	$E_{X_5^1, X_6^1}(X_8^1)$

   Alice对每个逻辑门这么做，然后把行的顺序打乱，全部发给Bob。

2. Alice把持有的输入发送给Bob。

   比如Alice已知$x_1=0, x_3=1$，那么就发给Bob$X_1^0, X_3^1$。Bob只知道密钥对应的线，但不知道原始值。

3. Alice通过不经意传输把Bob持有的输入对应的密钥发送给Bob。 Alice每次发送$(X_i^0, X_i^1)$，而Bob选择接受$x_i$对应的值。

4. Bob计算混淆过的电路的输出。 选择Bob有了所有输入对应的密钥，可以计算电路的结果。

5. Alice和Bob交换结果。 要么Alice把$X_7^0, X_7^1,X_8^0, X_8^1$对应的输入发送给Bob，要么Bob把计算结果发给Alice。

GMW

TODO: 搞懂

SHADE （Secure HAmming DistancE Computation ）

SHADE是一种基于$OT_1^2$(1-out-of-2 Oblivious Transfer) 计算汉明距离(Hamming Distance)的协议，我们这里介绍一种基本版的协议(The Basic Scheme)，同样在semi-honest环境下是安全的。

文中还介绍了另一种较为复杂的Fully Secure Scheme，在恶意环境下也是安全的。暂略。

一对一

Alice和Bob各自有长度为$n$的位串$X=(x_1,...,x_n), Y=(y_1,...,y_n)$，我们的目的使一方得到$X$和$Y$的汉明距离$d_H(X,Y)$而另一方什么都不得到。

1. Alice随机生成$n$个整数$r_1,...,r_n \in_R \Z_{n+1}$ 并计算$R=\sum_{i=1}^n r_i$。
2. 对于每个$i=1,...,n$, Alice和Bob进行一次 $OT_1^2$：
   • Alice发送 $(r_i+x_i, r_i+\overline{x_i})$
   • Bob选择 $b=y_i$并得到$t_i=r_i+(x_i \oplus y_i)$
3. Bob 计算 $T=\sum_{i=1}^n t_i$
4. Bob把$T$发送给Alice或Alice把$R$发送给Bob，接受方可以得到 $d_H(X,Y) = T - R$。

TODO：证明

一对多

类似地，我们可以高效地用SHADE计算一个$Y$和多个$X^1,...,X^N$的汉明距离。

1. Alice对每个$X^J$随机生成$n$个整数$r_1^j,...,r_n^j \in_R \Z_{n+1}$ 并计算$R^j=\sum_{i=1}^n r_i^j$。

2. 对于每个$i=1,...,n$, Alice和Bob进行一次 $OT_1^2$：

   • Alice发送并列的
     $$(r_i^1+x_i^1||...||r_i^1+x_i^N,r_i^1+\overline{x_i^1}||...||r_i^1+\overline{x_i^N})$$
   • Bob选择 $b=y_i$并得到
     $$(t_i^1||...||t_i^n)=t_i=(r_i^1+(x_i^1 \oplus y_i^1)||...||r_i^N+(x_i^N \oplus y_i^N))$$

3. Bob 计算 $T^j=\sum_{i=1}^n t_i^j$

4. Bob把$T^j$发送给Alice或Alice把$R^j$发送给Bob，接受方可以得到 $d_H(X^j,Y) = T^j - R^j$。

GSHADE

为了统一风格，这里用了和原论文不同的符号和公式。

目的

GSHADE协议的目的是在双方在不泄露输入的情况下，在其私有输入上交互计算一些距离量(distance metrics)，包括汉明距离、欧氏距离和点积等。 GSHADE可用于生物识别。服务器持有生物识别信息的数据库，而用户拥有个人数据。他们可以计算距离量，判断是否小于给定阈值来检查用户是否已经注册（存在于数据库中），而不透露他们的数据。

协议

我们可以推广SHADE到$\mathcal{F}^{GSHADE}$，所有可以被表示为

的函数，其中$Y$的定义域为长度为n的位串$Y=(y_1,...,y_n) \in \{0,1\}^n$，而$X$的定义域不受限制。可以简单理解为，可以分别用$X, Y$再通过$Y$的每一位和$X$做计算，并最终求和来得到结果的函数。

• 我们前面提到的汉明距离可以表示为 $f_X=f_Y=0, f_i(X, y_i) = x_i \oplus y_i$，所以属于$\mathcal{F}^{GSHADE}$。

• 点积(Scalar Product) 对于$X=(X_1,...,X_K)$, $X_i = (x_{K(i-1)+1},...,x_{K(i-1)+l})$以及$Y=(Y_1,...,Y_K)$, $Y_i = (y_{K(i-1)+1},...,y_{K(i-1)+l})$。我们有

  $$f_X=f_Y=0 \\ f_{K(i-1)+j}(X, y_{K(i-1)+j}) = 2^{j-1} \cdot X_i \cdot y_{K(i-1)+j}$$

• 平方欧几里得距离(Squared Euclidean Distance) 对于$X=(X_1,...,X_K)$, $X_i = (x_{K(i-1)+1},...,x_{K(i-1)+l})$以及$Y=(Y_1,...,Y_K)$, $Y_i = (y_{K(i-1)+1},...,y_{K(i-1)+l})$。我们有

  $$f_X=\sum_{i=1}^K (X_i)^2 \\ f_Y=\sum_{i=1}^K (Y_i)^2 \\ f_{K(i-1)+j}(X, y_{K(i-1)+j}) = -2^{j} \cdot X_i \cdot y_{K(i-1)+j}$$

一对一

GSHADE协议是在SHADE基础上改进的：

Alice和Bob各自有长度为$n$的位串$X=(x_1,...,x_n), Y=(y_1,...,y_n)$，我们的目的使一方得到$f(X,Y)=f_X(X)+\sum_{i=1}^n f_i (X, y_i) + f_Y(Y)$而另一方什么都不得到。

1. Alice随机生成$n$个整数$r_1,...,r_n \in_R \Z_{n+1}$ 并计算$R=\sum_{i=1}^n r_i-f_X(X)$。

2. 对于每个$i=1,...,n$, Alice和Bob进行一次 $OT_1^2$：

   • Alice发送 $(r_i+f_i(X,0), r_i+f_i(X,1))$
   • Bob选择 $b=y_i$并得到$t_i=r_i+f_i(X,y_i)$

3. Bob 计算 $T=\sum_{i=1}^n t_i + f_Y(Y)$

4. Bob把$T$发送给Alice或Alice把$R$发送给Bob，接受方可以得到

   $$f(X,Y) = f_X(X)+\sum_{i=1}^n f_i (X, y_i) + f_Y(Y) = T - R$$

一对多

类似地，我们可以高效地用GSHADE计算一个$Y$和多个$X^1,...,X^N$的距离量。

1. Alice对每个$X^J$随机生成$n$个整数$r_1^j,...,r_n^j \in_R \Z_{n+1}$ 并计算$R^j=\sum_{i=1}^n r_i^j - f_X(X_j)$。

2. 对于每个$i=1,...,n$, Alice和Bob进行一次 $OT_1^2$：

   • Alice发送并列的

     $$(r_i^1+f(X^1,0)||...||r_i^1+f(X^N,0),r_i^1+f(X^1,1)||...||r_i^1+f(X^N,1))$$

   • Bob选择 $b=y_i$并得到

     $$(t_i^1||...||t_i^n)=t_i=(r_i^1+f(X^1,y_i)||...||r_i^N+f(X^N,y_i))$$

3. Bob 计算 $T^j=\sum_{i=1}^n t_i^j + f_Y(Y_j)$

4. Bob把$T^j$发送给Alice或Alice把$R^j$发送给Bob，接受方可以得到

   $$f(X,Y) = f_X(X)+\sum_{i=1}^n f_i (X, y_i) + f_Y(Y) = T^j - R^j$$

比较

虽然GSHADE本身是用来计算数值而非比较，但由于Alice持有$R$而Bob持有$T$，我们很容易就可以利用混淆电路或者GMW来让两者合作计算比较电路。

应用与实验

一些生物识别算法是基于汉明距离或欧式距离的，所以我们可以应用GSHADE。

我使用GSHADE论文中提供的代码在两台2核4G的AWS Lightsail环境中进行了测试，GCC的版本为7.3.1。我使用了nethogs进行流量统计。另外原版的Makefile中编译器使用了-O3，我编译后运行时卡死，我改成-O2以后得到了正常的数据。

TODO: 虽然论文中说他们用了GMW表格中也写了GMW，但是他们提供的代码里似乎并没有GMW的部分？

SCiFi

SciFi是一个基于汉明距离的人脸识别算法，他将人脸照片提取为长度900的位串，两个照片的汉明距离就是两张脸的差异大小。

原论文是通过同态加密计算汉明距离，再通过OT得到是否距离是否小于阈值。由于同态加密是公钥加密，速度比较慢。这里是原文在Java环境下对于100张图片测试的结果

Offline preprocessing at the client took about 213 sec. Of this time, 38 seconds were spent on preparing 900 homomorphic encryptions, 71 seconds were used to send these encryption to the server, and 92 seconds were spent on running the preprocessing phase of the 1-outof-180 OT (which is used since we set dmax = 180).

而 Huang 提出了一种基于GC的协议，不仅计算更快，而且计算电路后直接加入比较电路得出结论，而不需要再进行OT。

Computing the Hamming distance between two 900-bit vectors took 0.019 seconds and used 56 KB bandwidth in the online phase (including garbled circuit generation and evaluation), with 0.051 seconds (of which the OT takes 0.018 seconds) spent on off-line preprocessing (including garbled circuit setup and the OT extension protocol setup and execution). For the same problem, the protocol used in SCiFI took 0.31 seconds for on-line computation, even at the cost of 213 seconds spent on preprocessing. 3 The SCiFI paper did not report bandwidth consumption, but we conservatively estimate that their protocol would require at least 110 KB.

TODO: 并没太看懂这里为什么是For the same problem，一个是两张图片对比而另一个是一个和一百个图片对比？但就算$(0.019+0.051) × 100$也比$213$小很多。

42使用了GMW，得到了如下的数据：

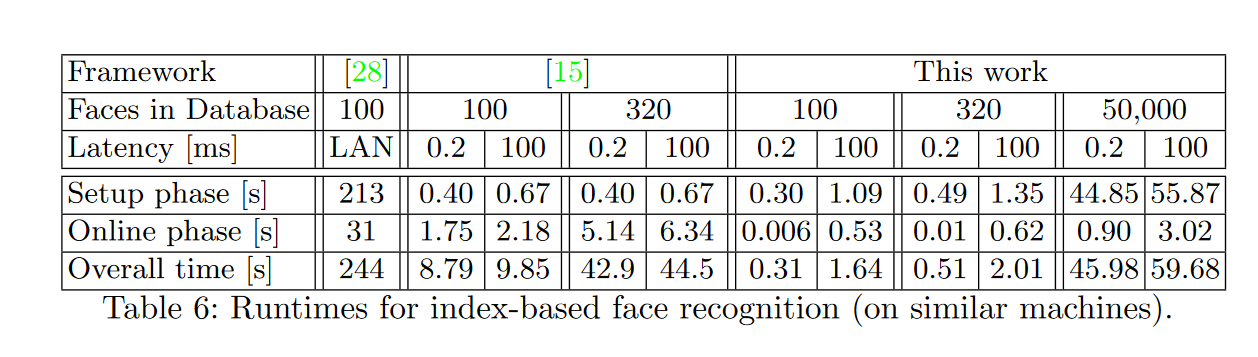
最后就是本论文用GSHADE的数据：

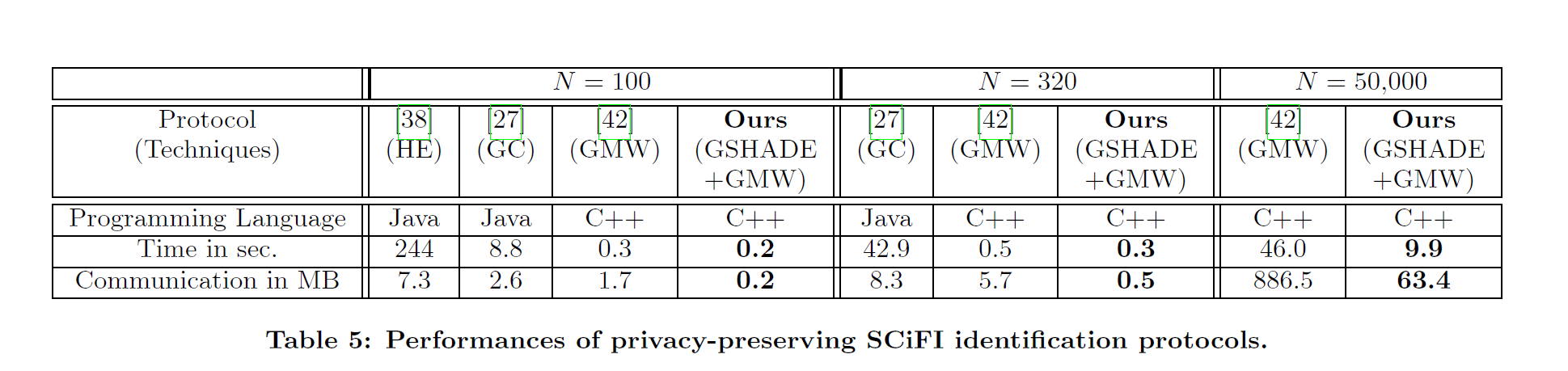
我实际测试后得到了以下的数据：

Required time for computing the 1-vs-100 Hamming distance on 900-bit elements: 0.016897s
0.124 MB

Required time for computing the 1-vs-320 Hamming distance on 900-bit elements: 0.060546s
0.366 MB

Required time for computing the 1-vs-50000 Hamming distance on 900-bit elements: 6.69268s
53.851 MB

可以看到时间和流量都比原文要少，推测是因为少了GMW对比的部分？

IrisCodes

IrisCodes 是一种基于 Normalized Hamming Distance 的虹膜识别协议。虽然计算过程中有除法 GSHADE 并不直接支持，但我们可以使用 GSHADE 分别计算分子和分母，再利用混淆电路或者GMW进行比较。

虽然论文中给出了如下的对比数据，但代码的README中提到The Normalized Hamming distance is currently not implemented, due to problems with the internal program structure. ，所以我也无从测试。

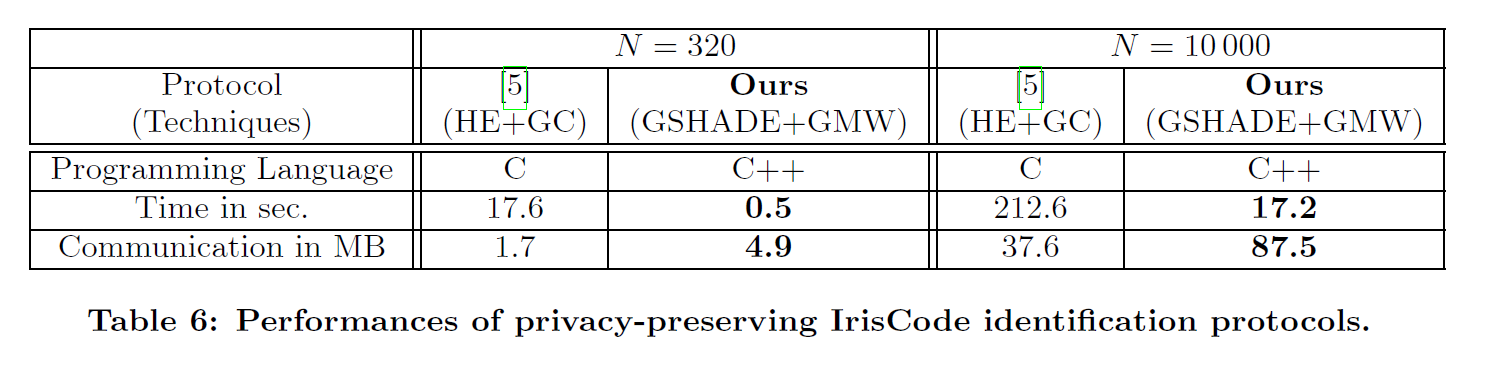
FingerCodes

FingerCodes 是一种基于欧式距离的指纹识别算法。作者对比的论文中采用了同态加密进行计算并使用混淆进行匹配

文中给出了如下的数据：

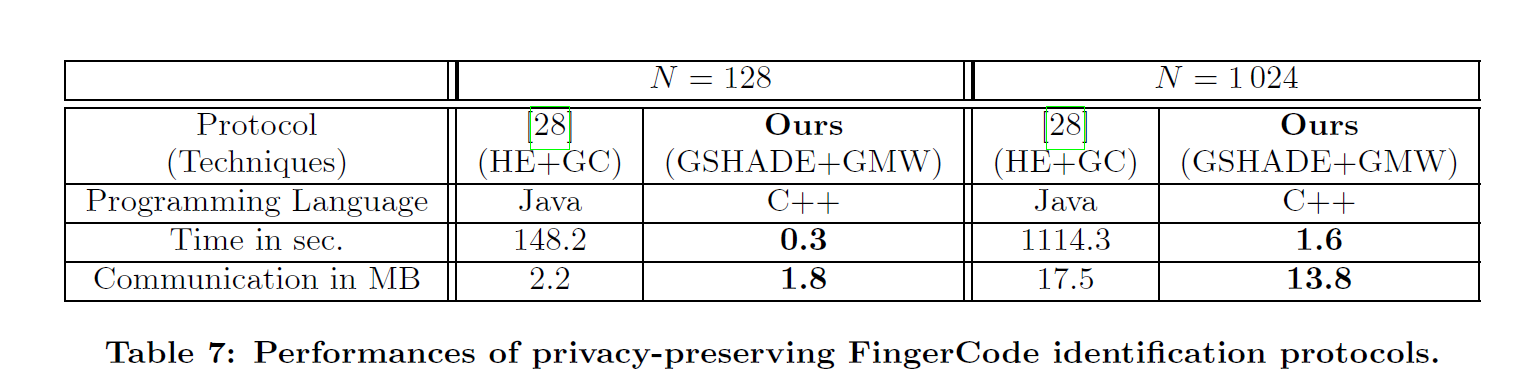
我实际测试后得到了以下的数据：

Required time for computing the 640-dimensional 1-vs-128 Euclidean Distance with 8-bit coordinates: 0.103081s
1.273 MB

Required time for computing the 640-dimensional 1-vs-1024 Euclidean Distance with 8-bit coordinates: 0.586264s
10.046 MB

可以看到时间和流量都比原文要少，推测是因为少了GMW对比的部分？

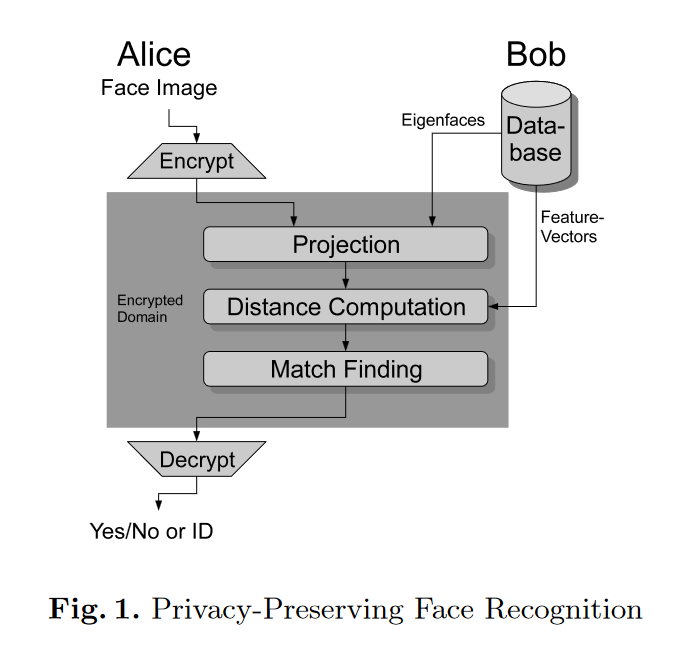
Eigenfaces

如图，Eigenfaces 需要在Projection用到点积在Distance Computation欧式距离，这两种算法都是GSHADE支持的。

最初的[18]中使用了同态加密，而[25]使用了同态加密和混淆电路（便于比较），再之后是[42]使用GMW。

文中给出了如下的数据：

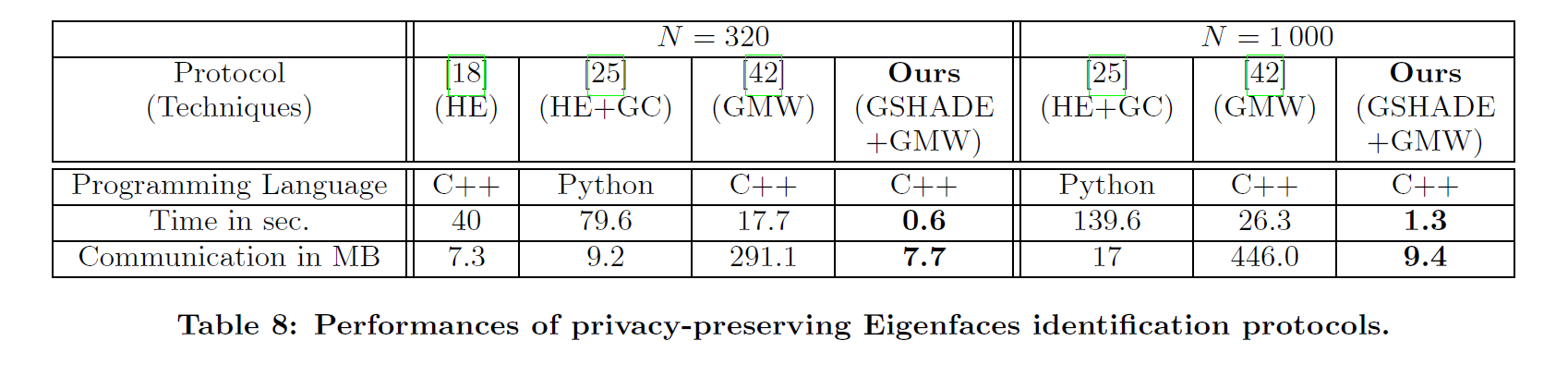
我实际测试后得到了以下的数据：

Required time for computing the Eigenfaces of a 10304 pixel image with 8-bit pixels and a 320-element database: 0.250193s
3.217 MB

Required time for computing the Eigenfaces of a 10304 pixel image with 8-bit pixels and a 1000-element database: 0.327062s
4.974 MB

可以看到时间和流量都比原文要少，推测是因为少了GMW对比的部分？

总结

可以看到我实验的时间和流量都比原文要少，推测可能是因为没有GMW比较的部分，如果加上GMW和原文提供的数据还是比较相符的。

参考

• 混淆电路介绍（一）不经意传输: https://zhuanlan.zhihu.com/p/126396795
• 混淆电路介绍（三）混淆电路原理: https://zhuanlan.zhihu.com/p/138371497
• GMW Protocol 介绍: https://zhuanlan.zhihu.com/p/237061306
• How to Exchange Secrets with Oblivious Transfer: https://eprint.iacr.org/2005/187.pdf
• More Efficient Oblivious Transfer and Extensions for Faster Secure Computation: https://eprint.iacr.org/2013/552.pdf
• SHADE: Secure HAmming DistancE Computation from Oblivious Transfer: https://eprint.iacr.org/2012/586.pdf
• GSHADE: Faster Privacy-Preserving Distance Computation and Biometric Identification: https://encrypto.de/papers/BCFPSZ14.pdf
• SCiFI – A System for Secure Face Identification: https://ieeexplore.ieee.org/document/5504789
• Faster secure two-party computation using garbled circuits: https://www.usenix.org/legacy/event/sec11/tech/full_papers/Huang.pdf